(1) 分散と標準偏差
$n$個のデータ$x_1$,$x_2$,$x_3$,$\cdots$,$x_n$の平均値を$\bar{x}$とします。
偏差(deviation)
各データと平均値の差を偏差といいます。
$i$番目のデータ$x_i$の偏差は$x_i-\bar{x}$で表せます。
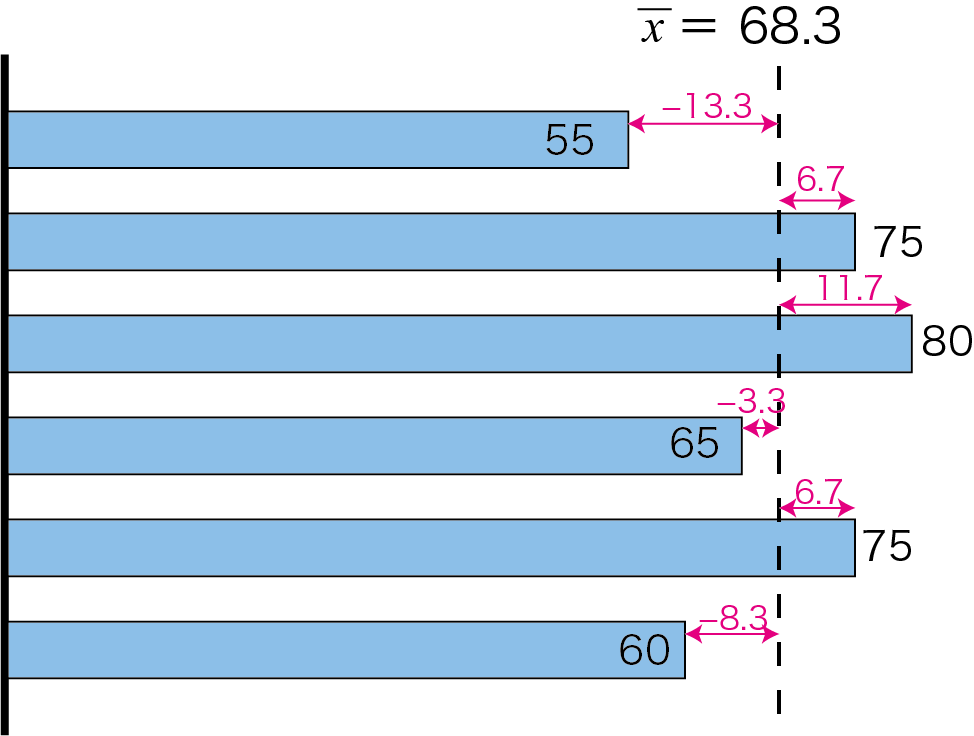
データのばらつきの度合いを表すのに、「偏差の平均値」を使いたいところですが、偏差には正の数もあれば負の数もあるので、平均すれば0(ゼロ)となり、データのばらつきの度合いを表すのには使えません。そこで、「偏差の2乗の平均値」とすることで、偏差が負の数の場合でも平均すれば0(ゼロ)とはならず、ばらつき度合いを表すことができます。
分散(variance)
データのばらつきの度合いを表す値を分散といいます。分散は、偏差の2乗の平均値です。分散$V$は次のように表すことができます。
\[ \begin{align*} V &= \frac{1}{n} \left\{ (x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \cdots + (x_n - \bar{x})^2 \right\} \\ \end{align*} \]
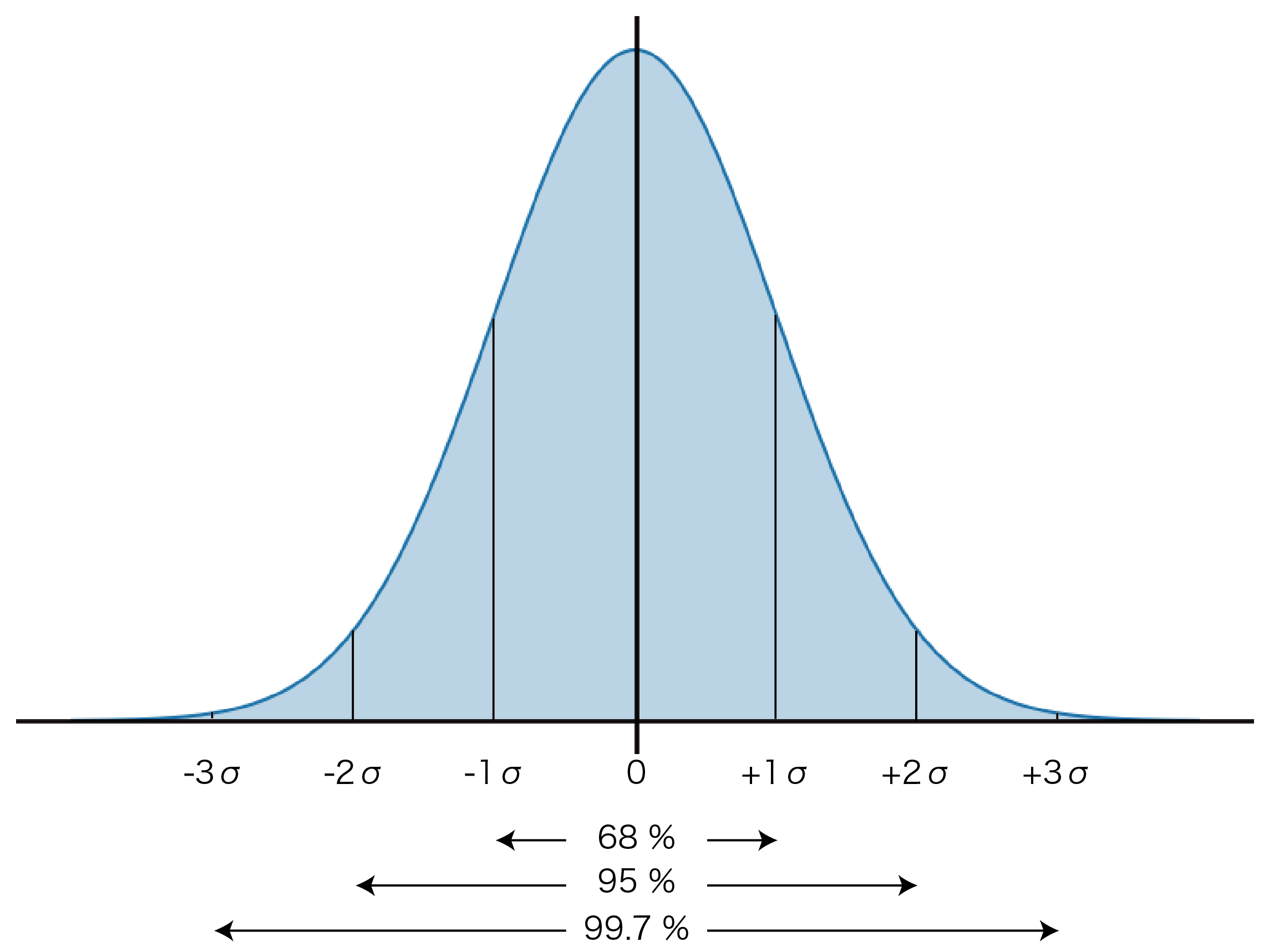
分散は元のデータの2乗なので、ばらつき度合いを表すことはできますが、各データが平均値からどれくらい離れているかを比較することはできません。そこで、分散の平方根を取って、データと比較できるようにしたので、次の標準偏差です。
標準偏差(SD: standard deviation)
分散の平方根をとった値を標準偏差といいます。標準偏差$\sigma$は次のように表すことができます。
\[ \begin{align*} \sigma &= \sqrt{V} = \sqrt{\frac{1}{n} \left\{ (x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \cdots + (x_n - \bar{x})^2 \right\} } \\ \end{align*} \]
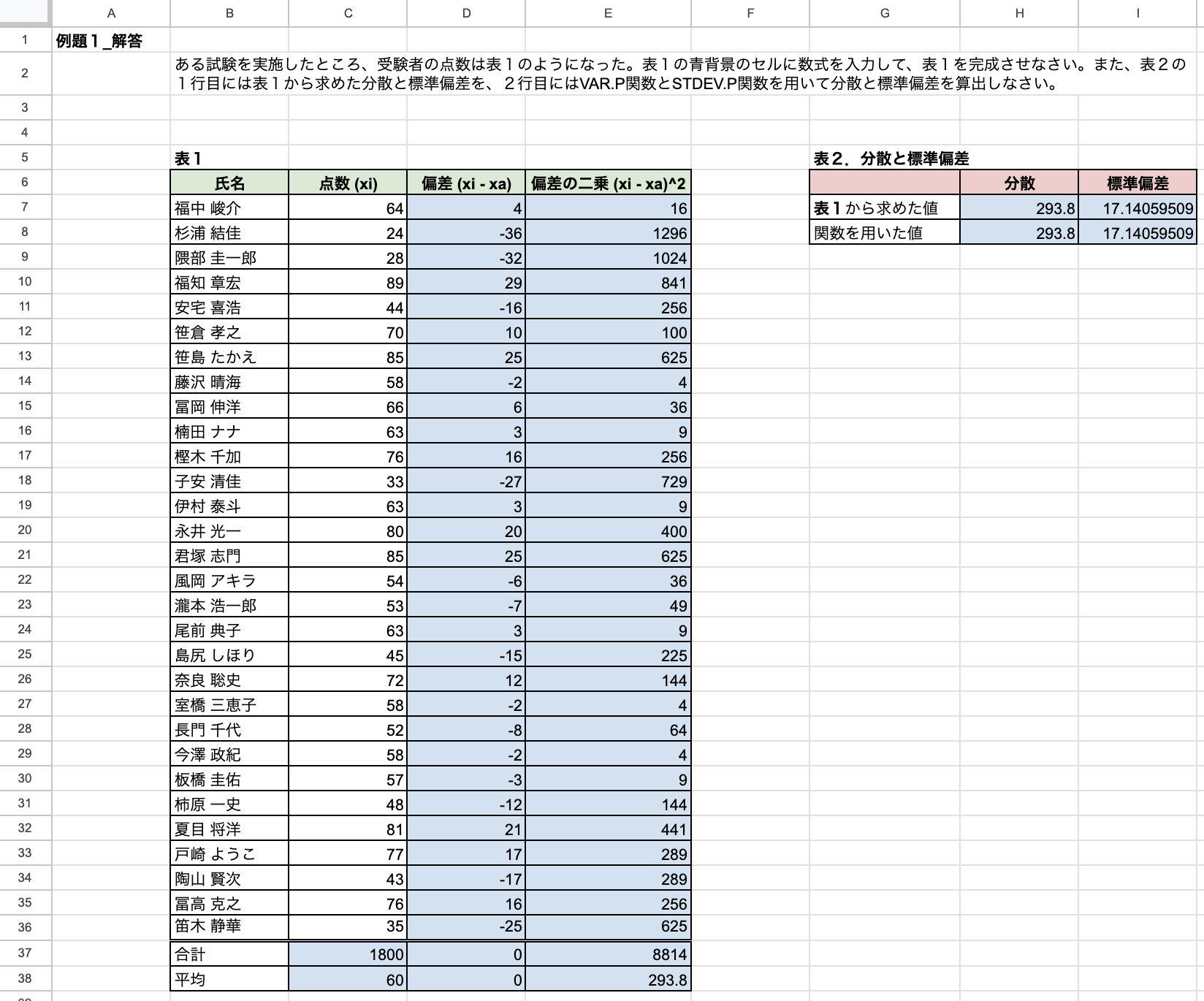
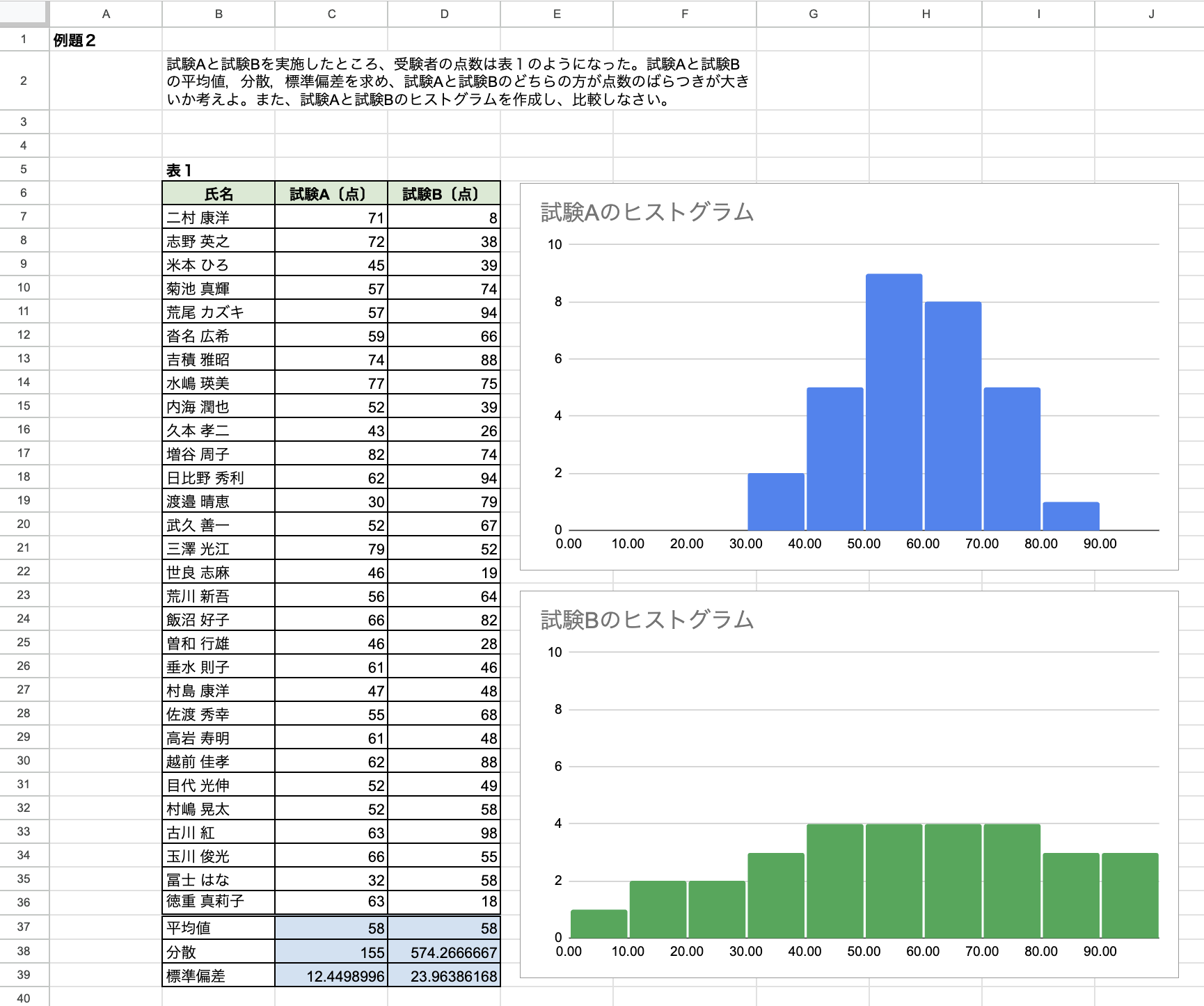
練習問題1
次表のデータについて、下の問いに答えよ。
| $x_i$ | 偏差 $(x_i - \bar{x})$ | 偏差の二乗 $(x_i - \bar{x})^2$ |
|---|---|---|
| 5 | 0 | 0 |
| 4 | -1 | 1 |
| 5 | 0 | 0 |
| 7 | 2 | 4 |
| 5 | 0 | 0 |
| 3 | -2 | 4 |
| 6 | 1 | 1 |
| 5 | 0 | 0 |
| 6 | 1 | 1 |
| 4 | -1 | 1 |
\[
\begin{align*}
\bar{x} &= \frac{5+4+5+7+5+3+6+5+6+4}{10} = 5.0\\
\end{align*}
\]
\[
\begin{align*}
V &= \frac{0+1+0+4+0+4+1+0+1+1}{10} = 1.2 \\
\end{align*}
\]
\[
\begin{align*}
\sigma &= \sqrt{1.2} \fallingdotseq 1.10
\end{align*}
\]
(1) 平均値$\bar{x}$を求めよ。
(2) 分散$V$を求めよ。
(3) 標準偏差$\sigma$を求めよ。
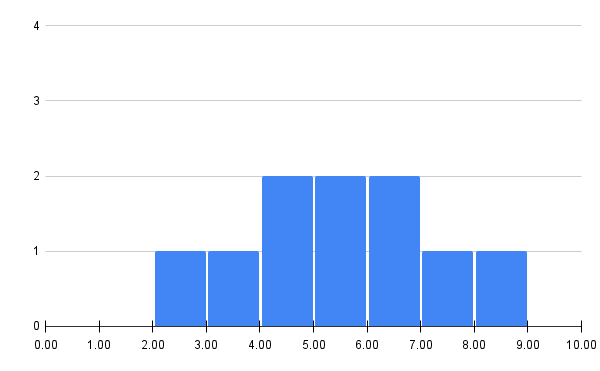
(4) ヒストグラムを作成せよ。
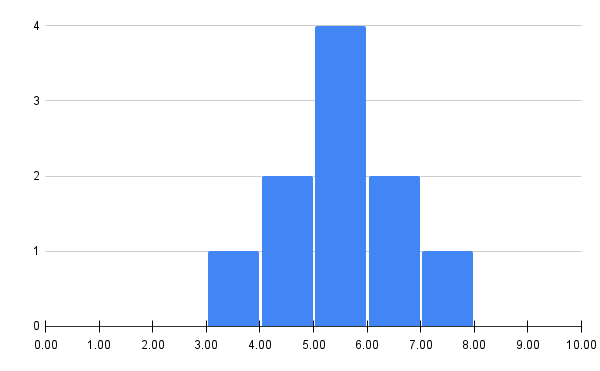
練習問題2
次表のデータについて、下の問いに答えよ。
| $x_i$ | 偏差 $(x_i - \bar{x})$ | 偏差の二乗 $(x_i - \bar{x})^2$ |
|---|---|---|
| 4 | -1 | 1 |
| 2 | -3 | 9 |
| 5 | 0 | 0 |
| 4 | -1 | 1 |
| 8 | 3 | 9 |
| 6 | 1 | 1 |
| 5 | 0 | 0 |
| 3 | -2 | 4 |
| 6 | 1 | 1 |
| 7 | 2 | 4 |
\[
\begin{align*}
\bar{x} &= \frac{4+2+5+4+8+6+5+3+6+7}{10} = 5.0\\
\end{align*}
\]
\[
\begin{align*}
V &= \frac{1+9+0+1+9+1+0+4+1+4}{10} = 3.0 \\
\end{align*}
\]
\[
\begin{align*}
\sigma &= \sqrt{3.0} \fallingdotseq 1.73
\end{align*}
\]
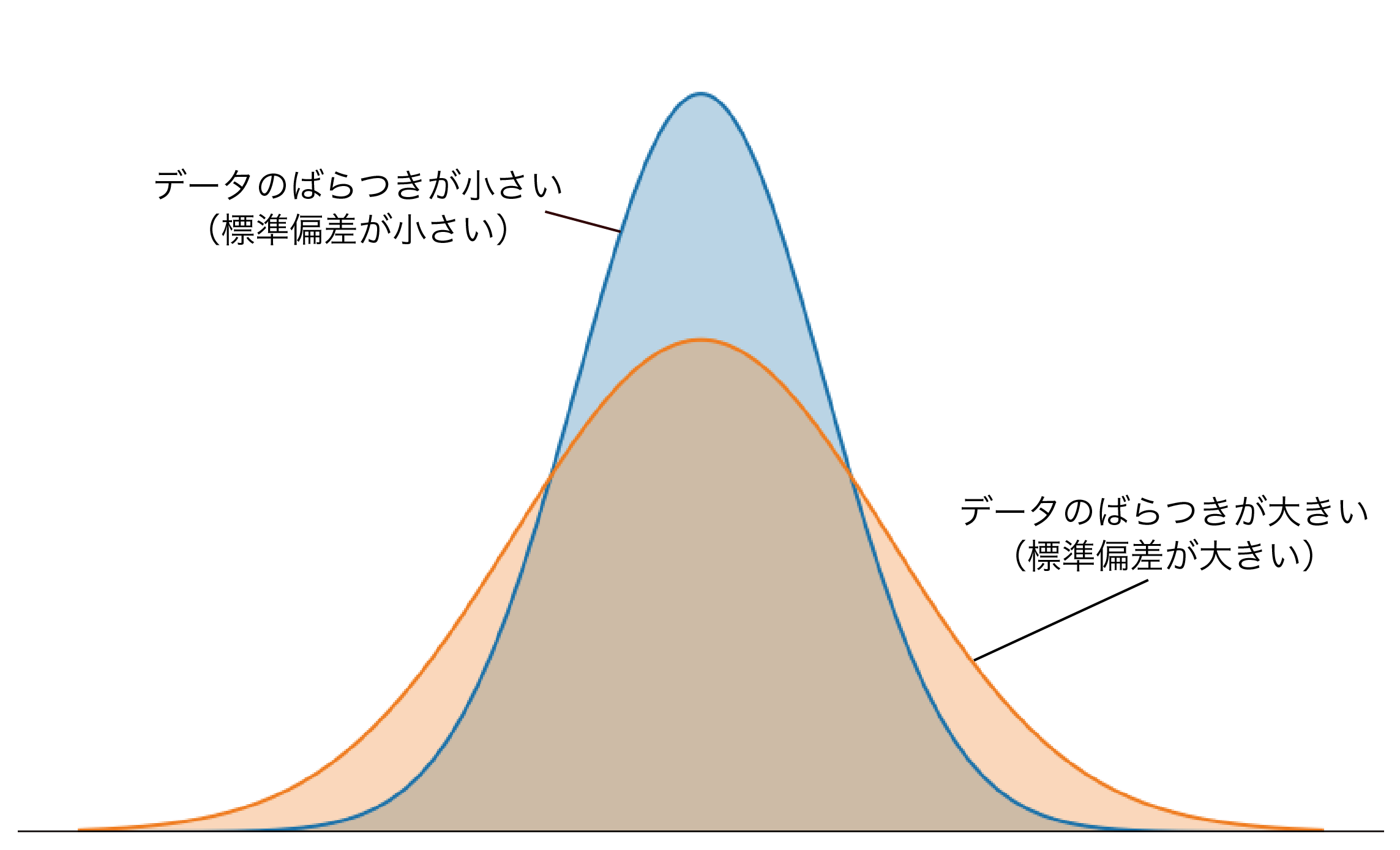
練習問題1と平均値は同じですが、標準偏差が大きいので、よりばらつきが大きい分布になっているのがわかります。
(1) 平均値$\bar{x}$を求めよ。
(2) 分散$V$を求めよ。
(3) 標準偏差$\sigma$を求めよ。
(4) ヒストグラムを作成せよ。