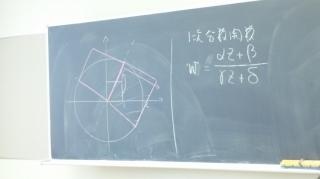第3回数学科リレー講座「複素数の世界」4日目
昨日までは、いわば「準備編」であったリレー講座。後半の三日間はいわゆる「複素関数論」の初歩を垣間見ます。
後半戦の初日は平山先生による「複素数平面上の幾何」と「複素数の関数」の解説です。まずは昨日の内容を復習された(写真1)あと、平面図形を複素数平面に配置して、複素数を利用した直交条件などを概観(写真2)。「複素数平面の上に置く？そんなことをしても大丈夫なのかなぁ…」といった感じの中1生が少なくなく、また受講者全体から「さすがにこれは前半戦よりは手強いぞ」という雰囲気がひしひしと感じられます。ちなみに、このリレー講座は他校からも先生が来訪されて、聴講されております(写真3)。
そして、いよいよ本講座の本題といえる複素関数の話題に突入しました(写真4)。
まずは一次関数を具体的に与え「幾何学的に」考察。果たして一次関数とは回転と平行移動の合成となることが示され(写真5)、大いに頷く中３生（数学部員の由）が印象的でした。
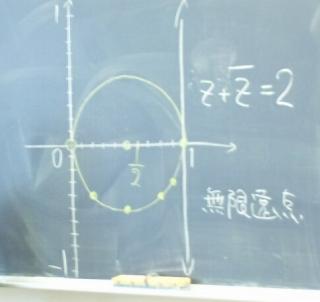
最後は一次分数関数にまで話題はおよび、具体例を用いて、いわゆる「円円対応」を解説されました。これは、複素数平面上の「円または直線」は一次分数関数によって「円または直線」に写ることを述べたものです。（写真6）に見ることのできる“無限遠点”の導入により，複素平面上の円は「リーマン球面」上の円と捉えることができることからこのように呼ばれているようです。
さすがに、時間の制約からリーマン球面についての詳しい言及はなされなかったのですが、このリーマン球面が明日のテーマの理解をするための鍵を握っています。
それにつけても、さすがに数学愛好者の集う本講座。欠席者が殆どいません。この調子でラストまで駆け抜けてください。(数学科)
（写真１）
（写真２）
（写真３）
（写真４）
（写真５）
（写真６）
【参加者の声】
高１ 東野哲君
今日は冒頭から未知の記号が頻発し、前途多難を感じさせましたが、具体例の計算を行うことで、漸く平山先生の主張されたことが理解できました。曰く言い難いのですが、授業の最後に説明された「円円対応」には深遠ななにかがあるのではないか、とにらんでいるのですが…（東野君、審美眼ありますね）。
このリレー講座は毎日違った先生が登場されるので日々新鮮な気持ちで授業を受けられるのがいいですね。80分があっという間です。
中３ 湯原卓也君
複素数ってすごいですね。平面図形の問題があんな感じで解決してしまうのですから。いよいよ準備が終わって本題ですね。今日は複素関数が楽しかったです。
【授業をしてみて】
今日のテーマは「複素数平面上の幾何」と「複素数の関数」の二つ。
前半では，複素数平面上に長さ，角度を導入して，図形の証明が複素数の計算でできることを。後半では，複素数平面から平面への関数を，具体的にグラフをかいてイメージをもってもらうことを目標に進めました。
今回の講座は，リーマン面，オイラーの公式，代数学の基本定理まで扱うという壮大な(無謀ともいえる)企画のもと，今日は複素数の関数のイメージだけでも何とか伝えて，あと２日のメインテーマにつながるようにしたいと思っていました。細かい計算や公式導出はバッサリ省いて，それでも講座前半で学んだ基本を復習すれば，後から十分読み返していけるような内容構成にしたつもりです。
1次分数関数のw=1/zにより直線が円に移されることを示すのに，簡単な計算から平面上に点を順にとってグラフを浮かびあがるようにした部分は，中学１年生レベルでも理解してもらえたのではないかと思います。複素数という道具を使うと実はいろいろなことができるんだ，ということから，ますます数学に興味をもってもらいたいと思います。
私自身は，従前のカリキュラムで扱った内容の復習をしながら，1次分数関数による円円変換の話など，当時はあまり授業では話さなかった部分の勉強ができ，楽しい講座準備期間でした。
（平山裕之）
